SDO_GEOMETRY
This is here for me to remember how much magic is used in inserting spatial (geometry) information into an Oracle database1.
CREATE TYPE sdo_geometry AS OBJECT (
SDO_GTYPE NUMBER,
SDO_SRID NUMBER,
SDO_POINT SDO_POINT_TYPE,
SDO_ELEM_INFO SDO_ELEM_INFO_ARRAY,
SDO_ORDINATES SDO_ORDINATE_ARRAY);
A point geometry:
MDSYS.SDO_GEOMETRY(
2001, -- 2-dimensional (2), non-linear referencing geometry or default (0), point (01)
28992, -- Amersfoort / RD New
NULL,
MDSYS.SDO_ELEM_INFO_ARRAY(1, 1, 1),
MDSYS.SDO_ORDINATE_ARRAY(81431.756, 455218.921))
A polygon geometry:
MDSYS.SDO_GEOMETRY(
2003, -- 2-dimensional (2), non-linear referencing geometry or default (0), polygon (03)
28992, -- Amersfoort / RD New
NULL,
MDSYS.SDO_ELEM_INFO_ARRAY(1,1003,1), -- first coordinate (1), exterior (1003), polygon (1)
MDSYS.SDO_ORDINATE_ARRAY(
-1041172.16,1407540.16,
-958596.8,-591471.68,
1363835.2,-625878.08,
1319106.88,1428184,
-1041172.16,1407540.16) -- coordinates
)
A multipolygon geometry:
MDSYS.SDO_GEOMETRY(
2007, -- 2-dimensional (2), non-linear referencing geometry or default (0), MULTIPOLYGON or MULTISURFACE (07)
28992, -- Amersfoort / RD New
NULL,
MDSYS.SDO_ELEM_INFO_ARRAY(1, 1003, 1, 11, 2003, 1),
MDSYS.SDO_ORDINATE_ARRAY(42, 78, 41, 85, 46, 82.7, 45, 79, 42, 78, 43.5, 72.5, 52.5, 72.5, 54.5, 79.5, 79, 60, 93, 46, 53, 32, 54, 25, 49, 22, 45, 17, 41, 16, 37, 23, 33, 24, 25, 20, 33, 46, 39, 53, 43.5, 72.5))
The only thing that makes sense among all the magic numbers are the coordinates. The last coordinate is the same as the first coordinate to close the polygon.
I since have found some more information after some digging regarding the SDO_ELEM_INFO.
It's an array of triplets, where a triplet consists of:
- SDO_STARTING_OFFSET
- offset within the coordinates array, the first triplet usually has "1" as being the first coordinate in the coordinate array
- SDO_ETYPE
- type of element
- SDO_INTERPRETATION
- depends on if SDO_ETYPE is a compound element
I found more information in [2].
WKT - Well-known text representation of geometry
"POLYGON ((194232.738 467652.498, 194232.774322728 467652.19885542, 194232.881179968 467651.917096035, 194232.738 467652.498))"
"POINT (31256.383 393077.6)"
"MULTIPOLYGON(((42 78, 41 85, 46 82.7, 45 79, 42 78),(43.5 72.5, 52.5 72.5, 54.5 79.5, 79 60, 93 46, 53 32, 54 25, 49 22, 45 17, 41 16, 37 23, 33 24, 25 20, 33 46, 39 53, 43.5 72.5)))"
It's possible to create SDO_GEOMETRY in PL/SQL based on WKT strings.
Like so:
SELECT SDO_GEOMETRY('MULTIPOLYGON(((42 78, 41 85, 46 82.7, 45 79, 42 78),(43.5 72.5, 52.5 72.5, 54.5 79.5, 79 60, 93 46, 53 32, 54 25, 49 22, 45 17, 41 16, 37 23, 33 24, 25 20, 33 46, 39 53, 43.5 72.5)))') FROM DUAL;
Convenient if you want to do something quick, but you cannot provide additional information regarding the dimensions, and coordinate system, etc.
Let me rephrase that sentence. It means your resulting geometrie has NO SRID, and you'll get in trouble using it in geometry queries! This is not a joke!
The reverse (if you want to find out the geometrie in WKT format, basically because it reads easier) is of course also possible, like so:
SELECT SDO_UTIL.TO_WKTGEOMETRY(geometry) FROM buildinggeo;
Geometry Functions
So I was playing around with ConvexHull, ConcaveHull and ConcaveHull-Boundary functions.
I took the MultiPolygon in the paragraph above as an example.
SELECT SDO_GEOM.SDO_CONVEXHULL(MDSYS.SDO_GEOMETRY(
2007, -- 2-dimensional (2), non-linear referencing geometry or default (0), multipolygon (07)
28992, -- Amersfoort / RD New
NULL,
MDSYS.SDO_ELEM_INFO_ARRAY(1,1003,1,11,2003,1), -- first coordinate (1), Simple polygon whose vertices are connected by straight line segments (1003,1), 11th coordinate (11), Simple polygon whose vertices are connected by straight line segments (1003,1)
MDSYS.SDO_ORDINATE_ARRAY(42, 78, 41, 85, 46, 82.7, 45, 79, 42, 78,
43.5, 72.5, 52.5, 72.5, 54.5, 79.5, 79, 60, 93, 46, 53, 32, 54, 25, 49, 22, 45, 17, 41, 16, 37, 23, 33, 24, 25, 20, 33, 46, 39, 53, 43.5, 72.5) -- coordinates
), 1)
FROM dual;
-- creates MDSYS.SDO_GEOMETRY(2003, 28992, NULL, MDSYS.SDO_ELEM_INFO_ARRAY(1, 1003, 1), MDSYS.SDO_ORDINATE_ARRAY(41, 16, 45, 17, 93, 46, 79, 60, 54.5, 79.5, 41, 85, 25, 20, 41, 16))
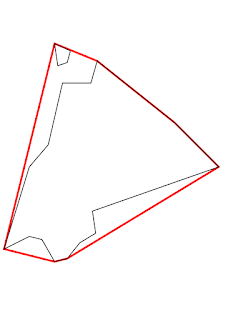
SELECT SDO_GEOM.SDO_CONCAVEHULL(MDSYS.SDO_GEOMETRY(
2007, -- 2-dimensional (2), non-linear referencing geometry or default (0), multipolygon (07)
28992, -- Amersfoort / RD New
NULL,
MDSYS.SDO_ELEM_INFO_ARRAY(1,1003,1,11,2003,1), -- first coordinate (1), Simple polygon whose vertices are connected by straight line segments (1003,1), 11th coordinate (11), Simple polygon whose vertices are connected by straight line segments (1003,1)
MDSYS.SDO_ORDINATE_ARRAY(42, 78, 41, 85, 46, 82.7, 45, 79, 42, 78,
43.5, 72.5, 52.5, 72.5, 54.5, 79.5, 79, 60, 93, 46, 53, 32, 54, 25, 49, 22, 45, 17, 41, 16, 37, 23, 33, 24, 25, 20, 33, 46, 39, 53, 43.5, 72.5) -- coordinates
), 0.1)
FROM dual;
-- creates MDSYS.SDO_GEOMETRY(2003, 28992, NULL, MDSYS.SDO_ELEM_INFO_ARRAY(1, 1003, 1), MDSYS.SDO_ORDINATE_ARRAY(41, 85, 42, 78, 43.5, 72.5, 39, 53, 33, 46, 25, 20, 41, 16, 45, 17, 54, 25, 53, 32, 93, 46, 79, 60, 54.5, 79.5, 46, 82.7, 41, 85))
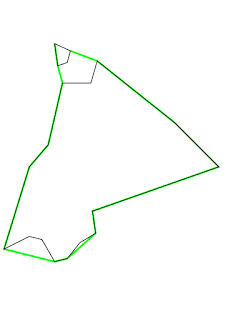
SELECT SDO_GEOM.SDO_CONCAVEHULL_BOUNDARY(MDSYS.SDO_GEOMETRY(
2007, -- 2-dimensional (2), non-linear referencing geometry or default (0), multipolygon (07)
28992, -- Amersfoort / RD New
NULL,
MDSYS.SDO_ELEM_INFO_ARRAY(1,1003,1,11,2003,1), -- first coordinate (1), Simple polygon whose vertices are connected by straight line segments (1003,1), 11th coordinate (11), Simple polygon whose vertices are connected by straight line segments (1003,1)
MDSYS.SDO_ORDINATE_ARRAY(42, 78, 41, 85, 46, 82.7, 45, 79, 42, 78,
43.5, 72.5, 52.5, 72.5, 54.5, 79.5, 79, 60, 93, 46, 53, 32, 54, 25, 49, 22, 45, 17, 41, 16, 37, 23, 33, 24, 25, 20, 33, 46, 39, 53, 43.5, 72.5) -- coordinates
), 0.1, 0.01)
FROM dual;
-- creates MDSYS.SDO_GEOMETRY(2003, 28992, NULL, MDSYS.SDO_ELEM_INFO_ARRAY(1, 1003, 1), MDSYS.SDO_ORDINATE_ARRAY(41, 85, 33, 46, 25, 20, 41, 16, 45, 17, 54, 25, 53, 32, 93, 46, 79, 60, 54.5, 79.5, 41, 85))
I will expand on this blog post, as my knowledge in this area is expanded.
References
- [1] Spatial and Graph Developer's Guide - 2.2 SDO_GEOMETRY Object Type
- https://docs.oracle.com/database/121/SPATL/sdo_geometry-object-type.htm#SPATL489
- [2] Spatial and Graph Developer's Guide - 2.2.4 SDO_ELEM_INFO
- https://docs.oracle.com/database/121/SPATL/sdo_geometry-object-type.htm#SPATL494
- Spatial and Graph Developer's Guide - 2.1 Simple Example: Inserting, Indexing, and Querying Spatial Data
- https://docs.oracle.com/database/121/SPATL/simple-example-inserting-indexing-and-querying-spatial-data.htm#SPATL486



